Math for ML - Linear Algebra

Ce post a pour but de me rappeler ce que j’ai appris durant la formation MOOC Coursera- Imperial College London : Mathematics for ML - Linear Algebra

Cours suivis au mois de Juin.

Certificat obtenu le 25 Juin 2021.

Cet article reprend l’organisation du cours et rappelle les objectifs de chaque chapitre.

Week 1: Introduction to Linear Algebra and to Mathematics for Machine Learning

Les objectifs :

• Recall how machine learning and vectors and matrices are related
• Interpret how changes in the model parameters affect the quality of the fit to the training data
• Recognize that variations in the model parameters are vectors on the response surface - that vectors are a generic concept not limited to a physical real space
• Use substitution / elimination to solve a fairly easy linear algebra problem
• Understand how to add vectors and multiply by a scalar number

SSR (Sum of Square Residual), une mesure d’adéquation, fit, entre le modèle et les données.

• Point 1: il est possible d’exprimer les paramètres d’un modèle sous forme de vecteur (i.e. [mu, sigma] pour une gaussienne)
• Point 2 : voir que les changements d’un modèle (ou paramètre du modèle), exemple une gaussienne, match plus ou moins bien les données
• Point 3 : exemple du domaine de définition d’une gaussienne [mu, sigma] qui forme une surface. Une variation Delta(mu,sigma) correspond à un vecteur sur la surface résultat.
• Point 4: élimination => \(ax+by=c\) et \(ax+dy=e\) on élimine les x substitution => on exprime x en fonction de y.

Week 2: Vectors are objects that move around space

Les objectifs :

• Calculate basic operations (dot product, modulus, negation) on vectors
• Calculate a change of basis
• Recall linear independence
• Identify a linearly independent basis and relate this to the dimensionality of the space

Ce chapitre rappelle comment on calcule :

• le module d’un vecteur,
• l’angle entre 2 vecteurs (dot product),
• et la projection d’un vecteur sur un autre.

Le module

Calcul du module d’un vecteur : \(|v| = \sqrt{a^2 + b^2 + ...}\).

Cette expression est déduite du théorème de Pythagore. Ceci se voit clairement sur un exemple en 2D.

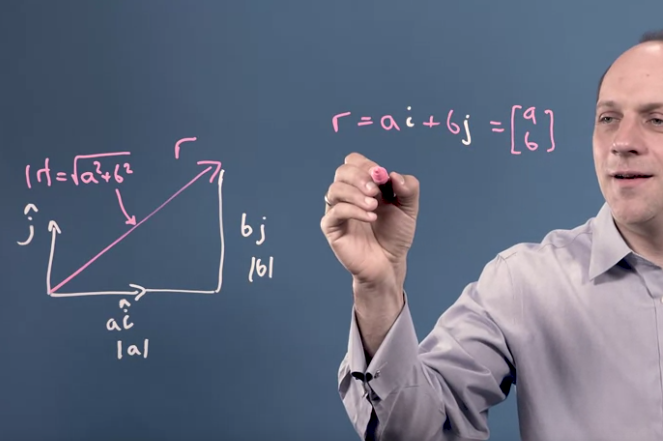
• module d’un vecteur valable même si base pas otho ?
• quel sesrait la signification de ca ?
• possible d’avoir un espace non eucliedien => où pythagore est != ?

Le Dot product

Le Dot Product a plusieurs autres dénominations possible :

• scalar product
• inner scalar product => produit scalaire
• projection product

Sa traduction semble être ‘produit scalaire’.

\[u.v = a1 * a2 + b1 * b2 + ...\]

Les propriétés du dot product :

• commutativité (invariabilité sur le sens, a.b = b.a)
• distributivité (l’addition (a+b).c = a.c + b.c)
• associativité (multiplication par un scalaire \(\lambda*(a+b) = \lambda*a + \lambda*b)\)

Projection d’un vecteur sur un autre : v sur u

Pour un vecteur en 2 dimensions.

\[u.v= |u|*|v|*cos(u,v)\]

car la loi des sinus dit :

\[c^2 = a^2 + b^2 - 2ab*cos(a,b)\]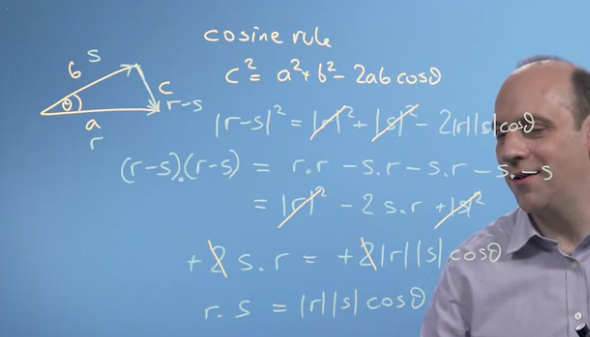

puis on passe aux vecteurs

puis ensuite la relation sohcahtoa \(cos(u,v) = \frac{adj}{hypotenus}\)

et \(u.v = |u|*|v|*cos(u,v)\) donne

\[adj = \frac{u.v}{|u|}\]

Ceci définit

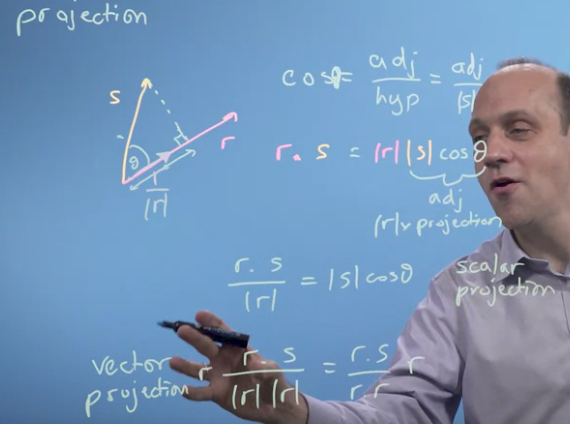
Le changement de base d’un vecteur.

Soit un vecteur u en base (a,b). exprimé par [A,B]

comment l’exprimer en base (c,d) ?

Projection de u sur c et d pour avoir les nouvelles coordonnées dans cette base.

\(u.c*\frac{c}{|c|}\) et \(u.d*\frac{d}{|d|}\)

mais pour que cela marche il faut que (c,d) soit orthogonaux.

car schema triangle rectangle et vecteurs.

sinon …pb …il faudrait faire un ‘transformation of axis’ en utilisant des matrices.

SCHEMA

Une base, décrit l’espace, ensemble de vecteurs linéairement indépendant c.a.d. pas une combinaison linéaire des autres.

dimension d’un espace.

Week 3: Matrices in Linear Algebra: Objects that operate on Vectors

Objectifs:

• Understand what a matrix is and how it corresponds to a transformation.
• Explain and calculate inverse and determinant of matrices
• Identify and explain how to find inverses computationally and what goes wrong.

Matrices vue comme une transformation.

Les colonnes sont les vecteurs d’arrivée des vecteurs de base. Exemple, SCHEMA

La Matrice Identité

La Matrice diagonale, qui transforme en rectangle

La Matrice diagonale avec 1 qui est minus, mirroir

\[A = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\]

mirroir plane

Une matrice inverse permet de calculer immédiatement toutes les valeurs pour un ensemble d’équations.

\[Ax=b\] \[A^{-1} * b = x\]

Matrice triangulaire

\[A=\begin{pmatrix} 1 & a & b \\ 0 1 & 1 & c \\ 0 & 0 & 1 \end{pmatrix}\]

est Echelon form

L’algorithme pour trouver l’inverse d’une matrice est simple : \(AA^{-1} = I\) donc résolution par pivot de Gauss.

Le déterminant

Le déterminant permet de dire de combien on aggrandit l’espace.

exemple qui etend le carré 1,1 vers un carré a,d a*d est le déterminant.

Pour une matrice 2x2

\[A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\]

ad-bc

L’inverse de la matrice est :

\[A^{-1} = \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}\]

multiplié par \(\frac{1}{dét}\).

Si dét = 0 alors la base n’est pas indépendante et A pas inversible car on projette vers un espace de dimension inférieure (e.g. l’ombre d’un objet 3D, 3D vers 2D), il n’est donc pas possible de faire la transformation inverse.

Week 4: Matrices make linear mappings

Objectifs :

• Identify matrices as operators
• Relate the transformation matrix to a set of new basis vectors
• Formulate code for mappings based on these transformation matrices
• Write code to find an orthonormal basis set computationally

Matrices as objects that map one vector onto another; all the types of matrices

Einstein Summation Convention : une façon d’écrire la multiplication de matrice avec une somme et les indices.

\[c_{ij} = \sum (a_{ik} * b_{kj})\]

Réexaminer le dot product comme la multiplication de 2 matrices (1 ligne et 1 colonne).

La projection d’un vecteur sur un autre, le dot product, peut aussi être vu comme une multiplication par une matrice.

Et donc, la projection d’un vecteur sur une nouvelle base comme une multiplication par une matrice.

Multiplication de matrices non carrées.

Matrice avec une dimension en moins permet de faire une projection, par exemple 3D vers 2D. exemple : SCHEMA

Matrices transform into the new basis vector set

Matrice de changement de base.

Passer d’un monde à un autre.

Exemple de la base du Panda.

On peut exprimer une matrice de transformation de vecteur exprimé dans la base de B vers notre base. Elle permet d’exprimer un vecteur V défini dans B vers notre monde.

\(B^{-1} * A * B\) avec B matrice de transformation de notre base vers la base de Panda A la transformation qu’on veut faire (rotation de 45 degrés). \(B^{-1}\) pour repasser de Panda à notre base.

Pour inverser une matrice 2x2.

\(A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\) devient \(\frac{1}{det} \begin{pmatrix} d & -b \\ -c & a \end{pmatrix}\)

Making multpiple Mappings, deciding if these are reversible

Matrice orthogonale, matrice orthonormé où les colonnes sont des vecteurs orthogonaux entre eux et de module 1.

Le déterminant d’une telle matrice est 1 ou -1 et \(A^{T} * A = I\).

Une matrice orthogonale toujours plus pratique : son inverse est sa transposée.

Multiplication … ???

Recognising mapping matrices and applying these to data

Gram-Schmid process pour transformer une matrice en base orthonormée :

Soit U = [u1,u2,…,un] ui les différents vecteurs de la base. E la base orthonormée.

Alors on prend le premier u1 et on le normalise \(e_1 = \frac{u_1}{|u_1|}\).

Ensuite on prend u2 et on le projette sur e1, il reste 1 composante en e2 avec e2 perpendiculaire à e1.

On normalise

On continu jusqu’à avoir notre base orthonormée.

Week 5: Eigenvalues and Eigenvectors: Application to Data Problems

Objectifs :

• Identify geometrically what an eigenvector/value is
• Apply mathematical formulation in simple cases
• Build an intuition of larger dimention eigensystems
• Write code to solve a large dimentional eigen problem

What are eigenthings

Un eigenvector d’une matrice est un vecteur qui conserve son orientation après application de la transformation.

Getting into details of eigenproblems

Calculer un eigenvector …

\[A*v = \lambda v\]

ce qui conduit à \(A-\lambda I = 0\)

apparement (???) pour ca il faut que det(A-lambdaI) = 0

ce qui conduit a un polynôme de l’ordre de la dimension de la matrice.

Résoudre ce polynôme (trouver les racines) permet de trouver les eigenvalues et par la suite les eigenvectors.

Montrer le process !!!

When changing to the eigenbasis is really usefull

Qu’est ce qu’une eigenbasis ? :

une base composées de eigenvectors d’une transformation.

Réécrire une transformation comme un passage vers sa eigenbasis puis revenir est très utile dans le cas où on veut appliquer n fois la même transformation.

\[A^n\]

car quand si on exprime A dans la eigenbasis Ae alors devient \(A = Ae * matriceEigenvalue\) Ae permet de passer dans l’espace défini par les eigenvecteurs et dans cet espace on sait que chaque dimensions est multiplié par une eigenvalue.

\[A = \begin{pmatrix} e_{1} & e_{1} & e_{1} \end{pmatrix} * \begin{pmatrix} eig_{1} & 0 & 0 \\ 0 & eig_{1} & 0 \\ 0 & 0 & eig3_{1} \\ \end{pmatrix}\]

ensuite pour revenir dans le premier espace on fait \(Ae^{-1}\).

\[A^n = Ae * \begin{pmatrix} eig1 & 0 & 0\\ 0 & eig2 & 0\\ 0 & 0 & eig3\\ \end{pmatrix}^n * Ae^{-1}\]

ce qui simplifie beaucoup les calculs si n est plutôt grand.

Making the PageRank algorithm

The PageRank algorithm va essayer de trouver un eigenvecteur d’une matrice exprimant un réseau de connexions entre pages.

Les valeurs de matrice sont le nombres de lien de la page i vers la page j. …

Exercices

Projeter un vecteur sur un autre

Exprimer un vecteur dans une autre base.